手撸神经网络 (1)

单个感知机

亲手撸个神经网络，所用到的解释和编程语言为：JavaScript 和 Processing。使用这两个语言的原因是，它们是图形可视化友好的。

建造一个神经网络，先从搞一个单个神经元/感知机开始。神经元之间相互联结起来，就组成了网络，神经元是构建摩天大楼的第一块砖。

一个神经元看起来长下面这样：

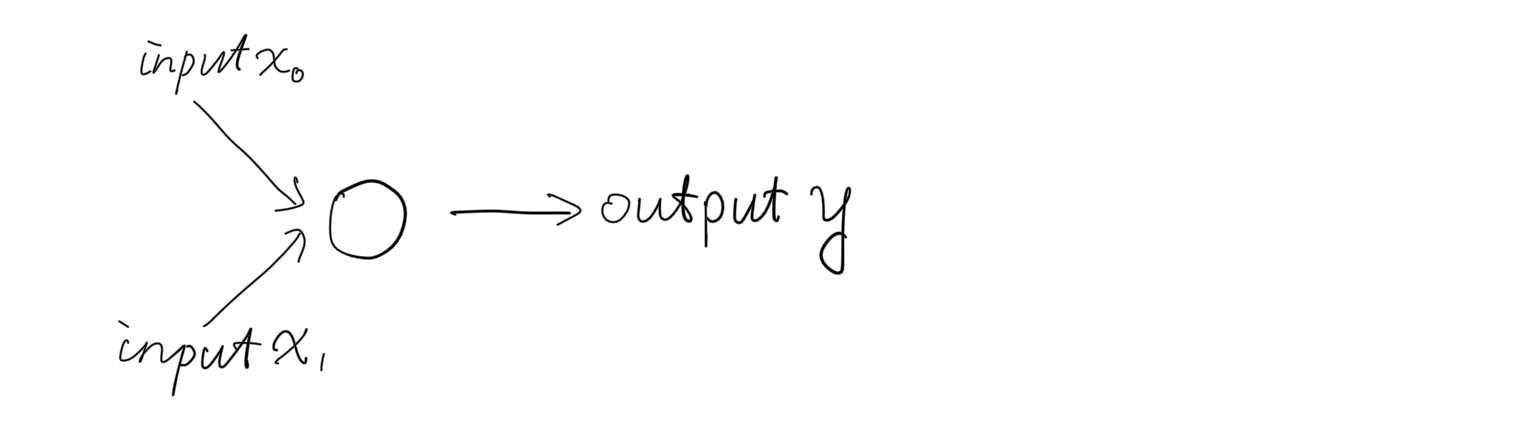
神经网络已经成为各种应用的标配，我们先搞个可以运行的低配：做一个二维空间里的二分类器。

通常，感知机负责接收输入，根据一个“预定义”的判别规则对输入进行求和，然后输出一个设定的值。象下面这样：

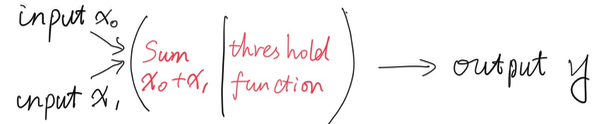
一个感知机能够接受无尽的参数，比如在图像分类当中，接受的参数个数是以千为单位的。我们先搞两个输入参数，因为两个参数可以被投射到二维空间里面，分别以x和y来表示，方便进行可视化。

从第一个包含着最最基础功能的神经元开始，让我们开始生命的进化之路。

这个最原始的神经元只做两件事：

把两个输入的参数加起来；
产生一个输出：-1 或者 +1，你可以理解为神经元最后的：不放电或者放电的决定。

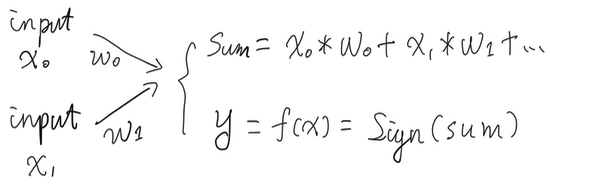
下面是实现的核心代码，用Processing编写:

class Perceptron {
  float[] weights;
  float learning_rate = 0.01; // a random picked value

  // Constructor, takes in # of weights and initialize
  Perceptron(int n) {
    weights = new float[n];
    for (int i = 0; i < weights.length; i++) {
      weights[i] = random(-1, 1);
    }
  }

  // Generate outputs
  int predict(float[] inputs) {
    float sum = 0;
    for (int i= 0; i < weights.length; i++) {
      sum += inputs[i] * weights[i];
    }
    int predict = sign(sum);
    return predict;
  }

  // Activate function, sign is a basic function gets "+" / "-"
  int sign(float sum) {
    if (sum >= 0) {
      return 1;
    } else {
      return -1;
    }
  }

}

感知机以如下方式工作:

Perceptron nn;

void setup() {
  size(400, 400);
  nn = new Perceptron(2);
  float inputs[] = {0.5, -1};
  // with bias version, there will be 3 inputs and 3 weights accordingly
  /*
  nn = new Perceptron(3);
  float inputs[] = {0.5, -1, 1}; // we give default value of bias: 1
  */
  int predict = nn.predict(inputs);
  println(predict);
}

void draw() {
}

Simply like that.

本节所涉及的数学知识

sum = w0*x0 + w1*x1 + ...
sign

Cite from wikipedia:

数和符号。每个数字都有多个属性：数值、符号和大小等。当一个实数的值（而非其大小）大于零时，我们称它为正数；当它小于零时，我们称它为负数。正负的属性被称为数的符号。

接下来看0：根据前面的公式：\(sum = weight * x\)，对每一个输入 x 乘以相应的权重wight。当 weight 或 x 为零时，y 可能等于 0。而对于 0，严格定义下的符号实际上无法适用，因此无法生成正或负的符号。带来的实际影响是，我们希望能够对于给定的对象进行二分类，比如一个工厂里生产出来的产品，区分为：好的/坏的; 合格的/不合格的等等，分别是+1 和 -1来表示。但是有一些产品，好像刚好坐落在分界线上面，它似乎既不好，也不坏，泾渭不那么分明。

我们在初中数学里学习过：\(y = kx\) 为正比例函数，它把平面空间一分为二，只不过这个函数有一个缺点(对于分类而言)，它只能生成一条经过坐标原点 (0, 0) 的直线。如果 x 为0，它只能返回 0，而0既不是正数，也不是负数，也就是无法区分。

很快，正比例函数之后，初中数学马上介绍了一次函数，y = kx + b。它是一个真正通用的公式，可以在二维平面上从任何方向绘制任何直线。其中 b 称为截距，当 b 不为0时，函数不经过坐标原点，也就完美地解决了无法对0进行分类的问题。

在神经网络中，我们也可以简单地为函数 \(sum = weight * x\) 增加“另一个”输入，称为“偏置”（bias）。偏置在实际应用中是一个固定的数值，并且具有其相应的权重。因此，感知机求和的公式变为：

\[sum = weight * x + weight * bias\]

偏置通常取值为“1”。通过上面的方法，我们消除了求和结果为零的影响，并得到了一个通用的二维线性分类函数：y = w * x + b。神经网络为何要选用看上去如此“简单”的一次函数？因为：它足够有效，并且计算量小。神经网络当然也可以采用复杂得多的函数表达式，但是当网络结构庞大到一定和程度，就会出现计算爆炸。

人在思考的时候，大脑的能耗并不会显著增加，约为17 ~ 20瓦，而预训练一个当前的大语言模型，在当前的算法设计和硬件条件下，所需的电量约为300万度。这就是自然进化在大脑上的卓越表现。