手撸神经网络 (2)

单个感知机和线性分类器

虽然现在还只是“单细胞生物”的形态，但我们即将赋予单感知机基本的功能：一个线性分类器。

如上图所示，蓝、绿点分别代表两个类别，红线划分出了分类的4个形态。解决这类问题，派出一个感知机就够了。

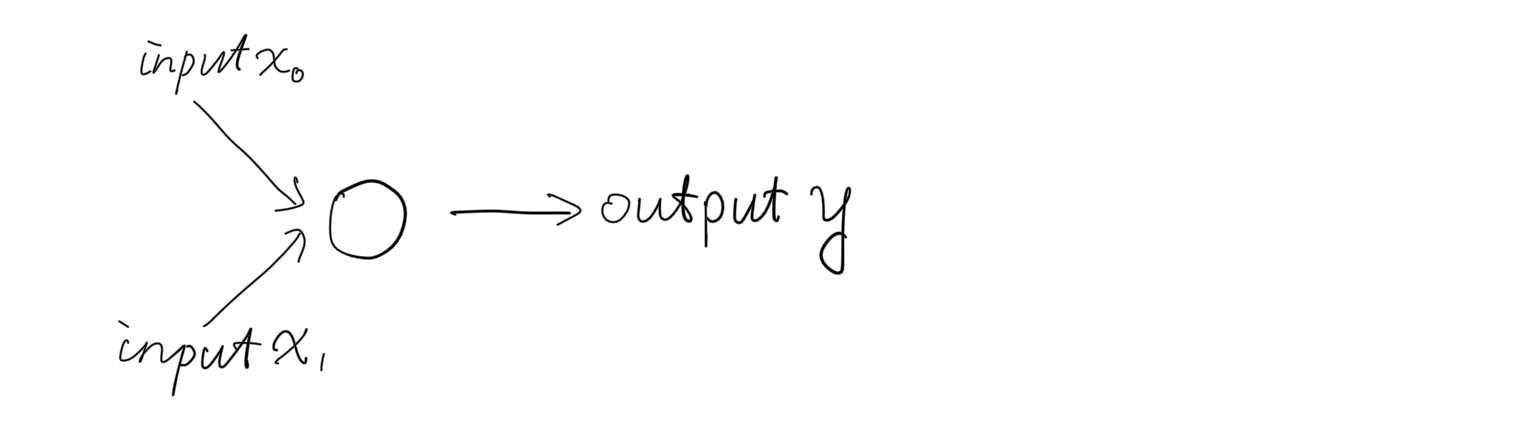
分类是机器学习中一种典型的“有监督学习”，这意味着算法对于预测对象的能力会被随时评估。当我们提到预测的能力时，通常指的是算法犯错误的程度。

让我们再次回顾一下输入和输出:

输入 (2个入参，所以选择两个入参是因为适应转化为x和y坐标从而表现为平面上的点的形式）；
权重 (初始化为-1~1之间的随机数值);
输出 (通过符号函数转化为-1和1);

目标是让感知机能够接受平面上的任意一点作为输入，输出分类的结果：-1 或者 1. 需要训练的参数是权重，使它能够帮助我们正确地分类。

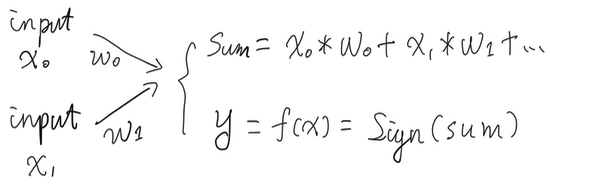
就好象开车的时候，重要的是确保行驶方向的正确性，在算法训练过程中，正确的方向来自于，对于“错误的评估”。

Actual	Predict	Actual - Predict
1	1	0
1	-1	2
-1	-1	0
-1	1	-2

以上是对于感知机对于输入和判断结果的四种状态的罗列，特别的，第2和第4行代表机器判断错误，即 “Actual” 和 “Predict” 不相符合。我们使用了一个简单的式子来描述错误的程度：

    Error = Actual - Predict

前面提到，权重是提升算法分类准确率的关键，我们对于权重的计算方式如下：

    Weights += Errors * Inputs * Learning_rate

Learning_rate 学习率是神经网络中的一个超参数, 代表着学习的速率, 简言之, 它是当前的权重向当前的错误的“屈服的程度”，它越倾向于承认当前的错误，那么它的学习的速度也将越快（然而这也并非全是好事，后面再展开）。

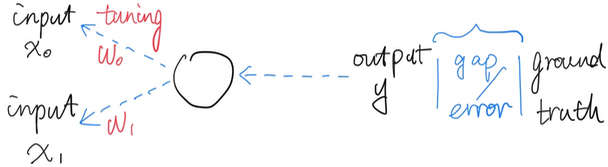
内部运作原理：

比较当前的输出和真实的分类结果，得到当前的错误程度，把错误信息向前（网络开始的地方）传递，进而对于权重进行调整，从而让最后的输出能够越来越符合输入的样本，神经网络中称为“反向传播”。

这一过程也典型地体现了，神经网络能够从“错误”中学习。

举个例子: 下面是一个前向传播的例子，2个输入分别是 0.5 和 1，两个随机赋予的权重分别是 0.1 和 -0.5，感知机输出的分类结果是 -1.

Inputs	Original weights	Sum(inputs * weights)	Sign outputs
0.5	0.1	0.5 * 0.1
1	-0.5	1 * -0.5
		0.05 - 0.5	-1

假如对于输入 0.5 和 1，期望的正确分类是1 而非上面的 -1，我们来看反向传播是如何对权重进行训练的：

Errors	Inputs	Learning_rate	New Weights	Original weights
1 - (-1)	0.5	1	2 * 0.5 * 1	0.1
1 - (-1)	1	1	2 * 1 * 1	-0.5

两个随机赋予的权重组合 0.1 和 -0.5，随着反向传播的进行，它们被调成了 1 和 2，尤其是后者，从-0.5被放大为2，也就是神经网络现在认为，后者(第2个输入)比前者更为重要。通过权重的调整，车子行进的方向也随之被调整了。

（注意: 为了方便演示，使用了 1 作为学习率，在实践当中，学习率通常是个远小于1的数值）

接下来代码实现:

在上一期代码的基础上，我们在感知机对象中添加一个训练函数：

class Perceptron {
  float[] weights;
  float learning_rate = 0.01;
  float bias = 1.0;
  
  // Constructor, takes in # of weights and initialize
  Perceptron(int n) {
    weights = new float[n];
    for (int i = 0; i < weights.length; i++) {
      weights[i] = random(1, 2);
    }
  }
  
  // Generate outputs
  int predict(float[] inputs) {
    float sum = 0;
    for (int i= 0; i < weights.length; i++) {
      sum += inputs[i] * weights[i];
    }
    int predict = sign(sum);
    return predict;
  }
  
  // Training process
  void train(int label, float[] inputs) {
    int predict_result = predict(inputs);
    int error = label - predict_result;
    if (predict_result == error) {
      return;
    }
    for (int i = 0; i < weights.length; i++) {
      // tune the weight based on previous result and basis
      weights[i] += inputs[i] * error * learning_rate;
    }
  }
  
  // used to plot classification line
  float guessY(float x) {
    //w0 * x + w1 * y + w2 * bias = 0;
    return -weights[2] * bias / weights[1] -weights[0] * x / weights[1];
  }
  
  // Activate function, sign is a basic function gets "+" / "-"
  int sign(float sum) {
    if (sum >= 0) {
      return 1;
    } else {
      return -1;
    }
  }
  
}

说明, 我们使用了输出 \(output = input *weight + bias* weight\) 在代码实现中，bias 预设为 1。

下面的动图说明了单个感知机是如何执行分类工作的，红点代表错误的分类，绿点代表正确的分类，黑色的线条代表分类函数，即之前所述的 \(y = kx + b\) 的形式。这个一次函数把整个2D平面一分为二，象征两个类别的分界线。红色表明了在神经网络在一次次迭代的过程中的学习过程。

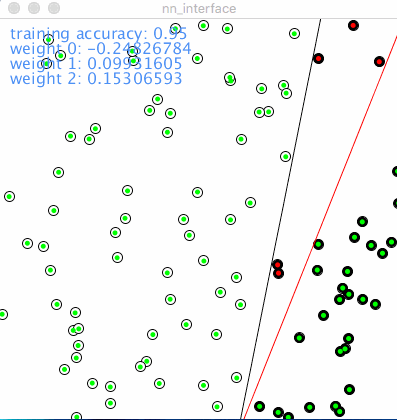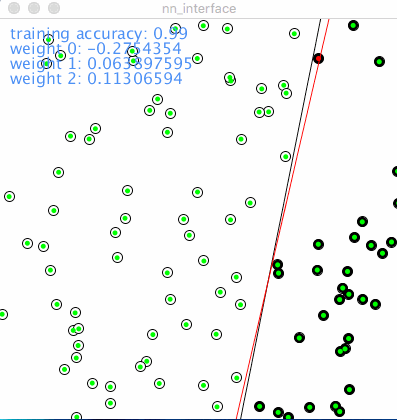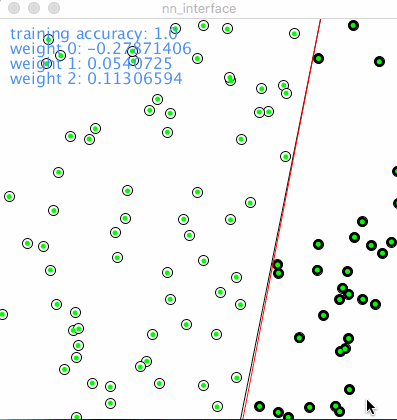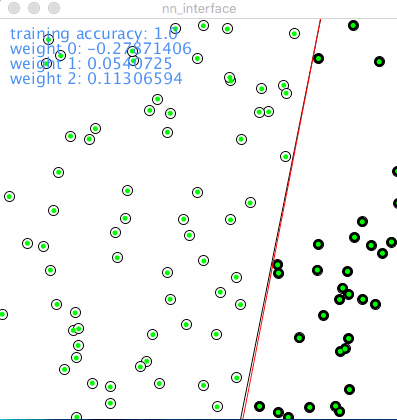
Learning rate 学习率决定了图中红线移动的速度和幅度，相对小的学习率占用了更多的训练时间，相对大的学习率则刚好相反。但是把学习率设得过大，将有可能使错过最优解。在训练大型神经网络的时候，经验之谈是，在起始把学习率调得大一些，然后再逐步调小，以期在学习速度和学习效果之间求取平衡。但是在实践中，学习率的设置仍然更象是一门“艺术”而非纯粹的“科学”。

通过把训练的过程可视化，我们还可以观察到更多有意思的现象，比如，在训练中我们对于权重的表达式：

Weight += error * learing_rate * input

为什么使用“ += ” 进行累加，如果把其中的 “+” 号移除，会发生什么？

Weight = error * learning_rate * input

下面的动图就是移除+号以后的训练过程，观察图中“红线”的移动路径：

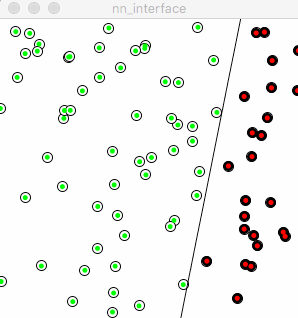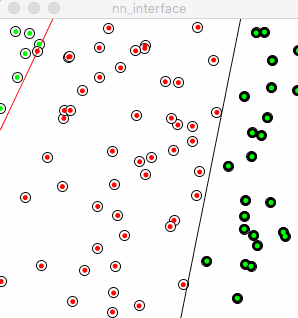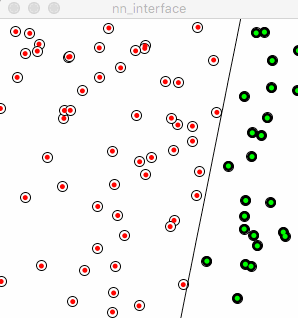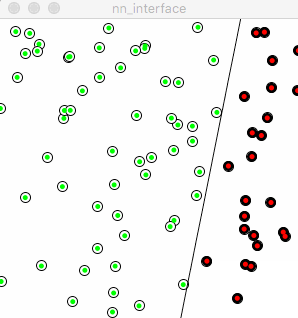
图中的“红线”看起来完全迷失了正确的方向，它的移动变得非常随机。反映在训练过程中，在去除了“+”号以后，感知机失去了从先前的错误中学习的能力，意味着每次它都是从头开始学起，而没有站在之前的自己的肩膀上。

原先代码中的小小的“+”，帮助了感知机能够慢慢地把先前的错误和经验积累起来，从而让自己慢慢地进步，这和人类的学习真像啊。

如你所见，这就是使用 Processing / JavaScript 等代码写神经网络程序的好玩的地方，可以通过自己调整代码，来观察整个训练过程，获得更直观的理解。

如果你想重现第一个动图中的结果，下面是使用的参数:

训练准确率: 从 0.95 到 1.0。在初始的100个点中，0.95意味着有5个点的类别被分错了，随着训练的进行被提升到百分之百的准确率。
权重0: 第一个输入的权重, -0.278
权重1: 第二个输入的权重, 0.054
权重2: 和bias相乘, 0.113

训练准确率帮助我们追踪训练过程的有效性，权重是从我们“喂”给神经网络的数据当中学习得到的。为了帮助进一步理解权重的含义，让我们随机写一个目标函数，然后看看神经网络如何执行它功能：线性拟合。

假设目标函数是: \(y = 5*x -2\) 即我们是根据此函数造出“训练数据”并喂给神经网络进行学习的。

根据:

\[weight_0*x + weight_1*y +weight_2*bias = 0\]

代入权重：

\(-0.278x + 0.054y + 0.113 = 0\) (bias取1)

化简整理：

\[54y = 278x - 113\] \[y = 5.148x - 2.09\]

和目标函数非常接近。

上述过程，目标是为了拟合一个函数，让最终的结果尽可能地接近目标函数。

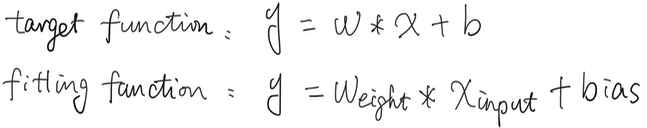
随着训练的完成，产出就是基于训练数据的权重数据，在线性分类器的情况下，就是拟合出的函数的斜率和目标函数的斜率尽可能相近。

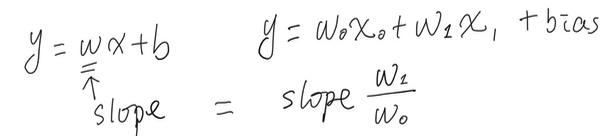
上面就是世界上最简单的神经网络，只有一个神经元的单个感知机，能够做的了不起的事情。如果我们手上有两个感知机，世界会有不同吗？