手撸神经网络 (4)
L1 和 L2 正则化
神经网络训练过程中,采用 L1 或 L2 正则化的目标是为了提高训练效率并避免过拟合。过拟合是指模型在训练数据上表现良好,但在未见过的数据上表现不佳的现象。
举个例子来说,深度学习领域最为成功的应用之一是图像分类。随着大量标注数据集的出现和大模型领域的进展,人们曾经预计:医院放射科医生的工作将被 AI 取代,因为 AI 在图像分类任务上表现优异。
然而,至少直到今天,这一预言并没有发生。现实情况是,如果用于诊断的片子的拍摄角度是模型没有见过的、或者片子过暗或者过于模糊,AI 模型的表现就会大打折扣。典型的做过的题目都会,没有遇见过的题目就不会了。
之前的文章实现了用一个简单的神经网络来解决 XOR 问题。现在,我们将通过引入 L1 和 L2 正则化来进一步提升模型的性能。
以下是 3 个具有不同隐藏节点数量的网络:
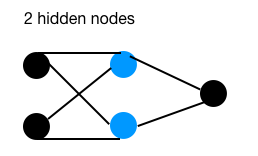
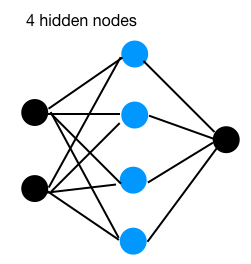
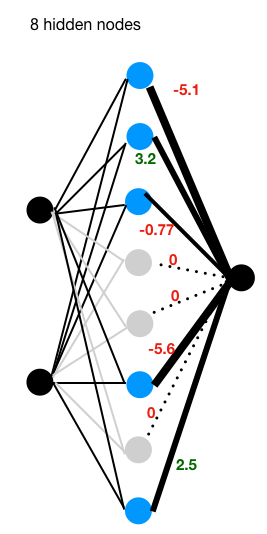
上述 3 个网络分别有 2、4、8 个隐藏节点,均为单隐藏层结构。我们使用相同的超参数(学习率、迭代次数等)进行训练。
目标是在训练集上达到 99% 的准确率。一旦达到目标,记录第 3 层的权重如下:
| hidden nodes | weights |
|---|---|
| 2 | 9.7 9.6 |
| 4 | -3.4 -4.5 -4.7 4.9 |
| 8 | -0.13 -0.58 -1.3 -1.3 -3.2 0.95 2.7 3.6 |
正如我们在之前的文章中测试过的:用于 XOR 问题的神经网络,包含 2 个隐藏节点的网络可以完成分类任务,尽管效率较低,大约每 10 次尝试中有 1 次成功。众所周知,当只有 2 个节点时,如果其中一个节点的权重方向错误,网络很难纠正到正确的方向上来。
对于 4 个隐藏节点的网络,它似乎能够很好地执行 XOR 问题,因为每次都能收敛到目标准确率,并以某种方式以相等的权重(绝对值)结束,这意味着所有 4 个节点都发挥了重要的代表作用。
当隐藏节点数量达到 8 时,与隐藏节点数量为 4 的结构相比,有 3 个节点(绝对权重接近零)。这意味着这 3 个节点在某种程度上是冗余的。
随着网络的加宽(单层中的隐藏节点增多)和加深(层数增多),它具有更强的表示能力。复杂的网络有利有弊,”更大”的网络面临更高的过拟合风险,并消耗更多的计算资源。
引入 L1 和 L2 正则化的目的是通过将一些“异常”权重压缩到接近零或等于零来最小化过拟合。在有“8 个隐藏节点”的第三张图中,在 L1 正则化项下,有 3 个节点(灰色)权重被设置为零,这意味着它们在网络中处于非激活状态,不会参与后续的前向和反向传播。对于剩下的 5 个节点,网络能够很好地执行 XOR 任务。
L1 正则化在某种程度上类似于第三张图中的“drop out”效果,在此不介绍所有避免过拟合的方法。
L1 regularization:
\[W = MSE + \lambda\sum_{i=1}^k|w_i|\]L2 regularization:
\[W = MSE + \lambda\sum_{i=1}^kw_i^2\]MSE 是均方误差,$w_i$ 是第 i 个权重,k 是权重的总数,$\lambda$ 是超参数,控制正则化的强度。 MSE 的计算方式如下: \(MSE = \frac{1}{n}\sum_{i=1}^n(y_i - \hat{y}_i)^2\)
其中 $y_i$ 是实际值,$\hat{y}_i$ 是预测值,n 是样本数量。
下表总结了 L1 和 L2 正则化的区别:
| Comparison | L1 regularization | L2 regularization |
|---|---|---|
| Computation | Inefficient on non-sparse | Efficient |
| Outputs | Sparse | Non-sparse |
| Feature selection | Yes, some set to 0 | No selection |
下面是一张来自于wikipedia的图片 wikipedia:
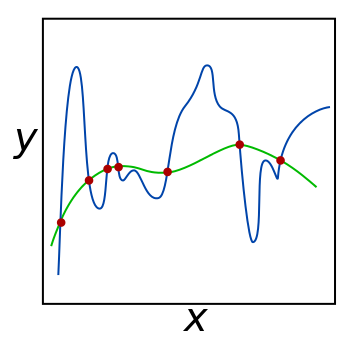
解释一下上图,假设我们有一些数据点(黑色点),我们想用一个函数来拟合这些数据点。绿色线是一个低阶多项式函数,蓝色线是一个高阶多项式函数。为了从另一个角度解释直觉,在图中,绿色线函数可以更好地对潜在的未知分布点进行泛化,而蓝色线似乎对每个单独的点过于敏感,从而导致过拟合。 (后面我可能会将图像更改为另一个更好的图像)。
假设绿色线的函数为:
\[y = 2 + 3x + 4x^2\]蓝色线的函数为:
\[y = 2 + 3x + 4x^2 + 5x^3 + 6x^4 + 7x^5\]在蓝色线的函数中,5、6、7 是我们想要消除的“异常”权重。换句话说,我们想要消除 5、6、7。在实际操作中,我们并不知道应该消除哪一个,我们所做的是将它们全部加起来,并对它们进行压缩。
对于 L2 正则化,我们对 5、6、7 进行平方处理(注意:这里的正则化项是为了说明原理,实际中应加到损失函数而不是模型输出):
\[\text{Loss} = MSE + \lambda(5^2 + 6^2 + 7^2)\]对于 L1 正则化,我们对 5、6、7 取绝对值(同样,正则化项应加到损失函数):
\[\text{Loss} = MSE + \lambda(|5| + |6| + |7|)\](其中 $w_1=5, w_2=6, w_3=7$,即为需要正则化的权重。)
在进行“压缩”处理时,对于 L1,一些特征/权重将被设置为零,我们可以认为 L1 是在参数更新(梯度下降)过程中,每次对权重减去一个固定的小数值;而对于 L2,一些权重将被设置为非常接近零但不会为零,我们可以认为 L2 是在参数更新时,每次对权重乘以一个小比例因子。这种区别体现在梯度更新步骤,而不是直接对权重进行操作。
这里的 $\lambda$ 是超参数,如果设置为零,则意味着没有正则化;如果设置为无穷大,我们得到的可能是所有权重都被设置为零(但实际训练中不会将 $\lambda$ 设置为无穷大,通常通过调参获得合适的值)。就像上面的函数,它将变为:
\[y = 2\]这意味着无论输入是什么,输出都是 2。它是一条平坦的线,模型走向了另一个极端方向:没有表示能力,也就是欠拟合。
作为一个经验法则,L1 正则化更适用于特征选择,而 L2 正则化更适用于处理多重共线性问题(即多个特征之间高度相关,导致模型难以区分它们的独立影响,例如房价预测中“房屋面积”和“房间数量”可能高度相关,L2 正则化可以帮助缓解这种情况)。 通过 L1 或 L2 正则化,我们可以在提升模型表达能力的同时,有效控制模型复杂度,增强泛化能力,避免因模型过于复杂而导致过拟合。实际应用中,可以通过交叉验证等方法合理选择隐藏节点数量、正则化方式和超参数 $\lambda$,以获得最佳的模型性能。