Dummy Deep Learning

手撸神经网络 (3)

XOR 异或问题

之前的练习中，我们实现了一个线性分类器，如下图所示，它可以在二维空间中分割两个类别。

然而这是最最简单的分类器。在现实世界中，单个线性分类器的能力不足以帮助我们解决如下问题：

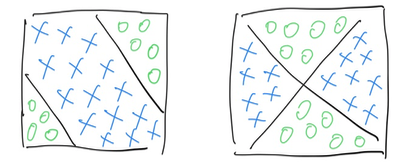
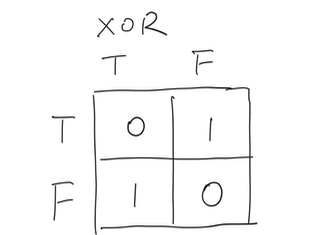
在计算机语言中，以上场景属于：XOR 异或问题。 XOR 是一个典型的非线性问题，依靠单个感知机无法解决。XOR 问题的特点是，两个输入的组合无法通过单一的线性分割来解决。

为了解决 XOR 问题，我们的网络将向前小小地迈进一步，从一个神经元（“单细胞生物”），向下图所示两个神经元的结构发展。

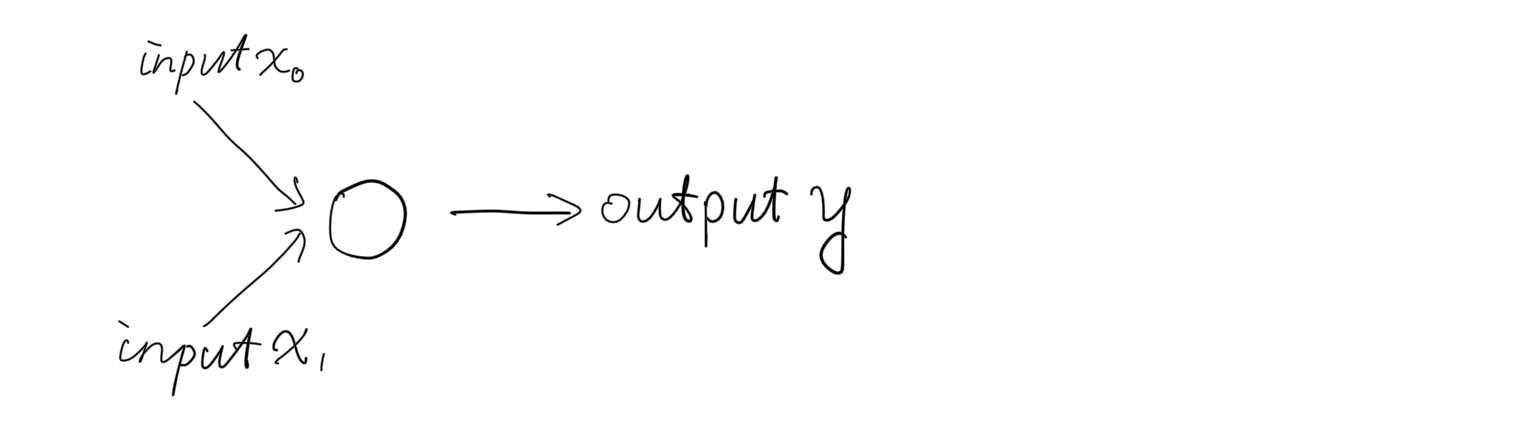
升级到两个神经元，即图中蓝色部分所示。

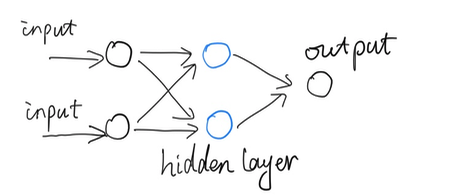
网络现在由 3 层组成：输入层、隐藏层和输出层，我们将蓝色部分称为神经网络的隐藏层。尽管网络结构发生了一点小变化，但是理念保持不变，依然通过前向传播向前传递信息。

每个层的网络节点与相邻层的节点进行通信。

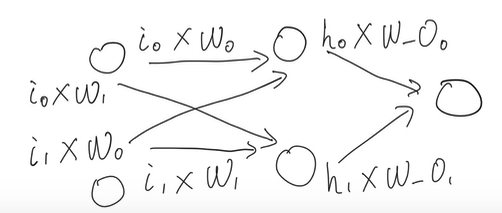
关于训练过程，我们将引入一个新术语：反向传播。

这一个部分涉及求导，即描述函数在某一点的变化率，以帮助我们理解函数的斜率和曲线的形状。和前面两节的内容不同，它需要微积分的知识，无法帮助初中生理解。

反向传播是一种用于训练神经网络的算法，通过计算损失函数相对于每个权重的梯度来更新权重。通过反向传播，我们可以计算出每个权重对输出的影响，从而调整权重，使输出朝着期望方向移动。反向传播的发明，使得深度神经网络的训练成为可能，从而使深度学习能够真正落地应用。而数学求导的引入，使得这一切变得更加高效，解决了计算复杂度的问题。

在之前的帖子中，对于简单的单层感知机神经网络，我们将误差定义为：

    Error = Actual - Predict
    weights += learning_rate * error * inputs

即使我们现在有了包含多个隐藏层的网络，误差的计算公式依然相似：

    delta_weight = learning_rate * error * gradient(1) * inputs(2)

保持足够的简单，才有最大的实用空间。

(1): 介绍梯度的目的是为了找到一个有效的优化斜率。 我们有一个方便的方式计算梯度：

\[s'(x)= s(x) * (1-s(x))\]

以 sigmoid 函数为例，对它进行求导：

\[s(x) = sigmoid(x) = \frac{1}{1+e^{-x}}\] \[let \: t = 1 + e^{-x}\] \[\frac{d(s)}{d(t)} = -t^{-2}\] \[\frac{d(t)}{d(x)} = -e^{-x}\]

根据链式法则，我们可以得到：

\[\frac{d(s)}{d(x)} = \frac{d(s)}{d(t)} * \frac{d(t)}{d(x)}\] \[\frac{d(s)}{d(x)} = -t^{-2} * -e^{-x} = \frac{e^{-x}}{t^2}=\frac{e^{-x}}{(1+e^{-x})^2}\]

又因为：

\[1 - s(x) = \frac{e^{-x}}{1+e^{-x}}\] \[s(x) = \frac{1}{1+e^{-x}}\]

所以上式可以简化为：

\[s'(x)= \frac{e^{-x}}{(1+e^{-x})^2} = s(x) * (1-s(x))\]

我们可以看到，sigmoid函数的导数，在计算上很简单的。sigmoid是神经网络激活函数选择里的常客，因为它的导数计算简单且具有良好的数学性质。

从函数图像看，sigmoid函数长得类似于一个压扁的S形曲线，输出值在0和1之间。

当sigmoid的值接近0或1时，导数的值接近0，函数的变化比较平缓，意味着在这些区域，网络的学习速度会变慢。从实际情况看，当sigmoid的值接近0或1时，网络的输出已经非常接近于目标值，因此不需要太多的调整。

当sigmoid的值接近0.5时，导数的值最大，意味着在这个区域，网络的学习速度最快。 此时导数的值为0.25，从实际情况看，当sigmoid的值接近0.5时，网络的输出最不确定，因此需要更多的调整。

现在让我们实现反向传播过程：

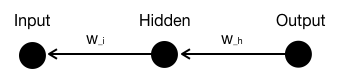
假设我们有一个简单的神经网络，包含由1个节点组成的输入层(I)、1个隐藏层(H)和输出层(O)。

假设目标输出为 “1” 或 “0”，记为 “Y”，我们可以得到误差或代价为：

\[Error = (O_{utput-activated} - Y)^2\] \[O_{utput-activated} = \sigma (H_idden * W_h + Bias)\] \[\sigma = \frac{1}{1 + e^{-x}}\] \[O_{utput} = H_idden * W_{hidden} + Bias\]

我们使用了 sigmoid 作为激活函数。 我们进行反向传播的目的是为了衡量“权重”对输出的影响，进而通过调整权重，使输出朝着“期望”方向移动。

假设输入层的输入为 Input，隐藏层的权重为 W_h，输出层的权重为 W_o，偏置为 Bias_h 和 Bias_o。

我们需要计算每个权重对误差的影响。下面是如何计算 “W_h” 对输出的影响：

\[\frac{\partial Error}{\partial W_h} = \frac{\partial Error}{\partial O_{utput-activated}} * \frac{\partial O_{utput-activated}}{\partial O_{utput}} * \frac{\partial O_{utput}}{\partial W_{hidden}}\]

这就是我们所说的“链式法则”。接下来实现链式法则：

\[\frac{\partial Error}{\partial O_{utput-activated}} = 2(O_{utput−activated} −Y)\] \[\frac{\partial O_{utput-activated}}{\partial O_{utput}} = \sigma'\] \[\sigma'(x)= \sigma(x) * (1-\sigma(x))\] \[\frac{\partial O_{utput}}{\partial W_{hidden}} = Hidden\]

现在放入学习率，并暂时忽略常数2，公式变为：

\[\frac{\partial Error}{\partial W_{hidden}} = learningrate * (O_{utput−activated} −Y) * \sigma(x) * (1-\sigma(x)) * Hidden\]

计算 “W_i” 对输出的影响：

\[\frac{\partial Error}{\partial W_i} = \frac{\partial Error}{\partial H_{idden-activated}} * \frac{\partial H_{idden-activated}}{\partial H_{idden}} * \frac{\partial H_{idden}}{\partial W_{input}}\] \[\frac{\partial Error}{\partial H_{idden-activated}} = 2(O_{utput−activated} −Y) * W_{hidden}\] \[\frac{\partial H_{idden-activated}}{\partial H_{idden}} = \sigma'\] \[\sigma'(x)= \sigma(x) * (1-\sigma(x))\] \[\frac{\partial H_{idden}}{\partial W_{input}} = Input\]

现在继续放入学习率并忽略常数2，公式变为：

\[\frac{\partial Error}{\partial W_{input}} = learningrate * Error * W_{hidden} * \sigma(x) * (1-\sigma(x)) * Input\]

关于反向传播，一个很好的在线教程是Andrej Karpathy 主讲的 cs231n 。

我们已经完成了反向传播的实现。以后扩展到多节点的深层神经网络，方法论也同样适用，只需要将相应的误差和前一层的值相加即可。

反向传播的过程是计算导数的一种方式，我们应该感谢导数这一强大工具，尽管深度神经网络计算量非常繁重，但它帮助我们节省了大量时间，使深度神经网络的计算变得可能。

(2):

在实现中，我们使用矩阵运算来处理输入、权重和偏置。以下是一个简单的实现示例，使用了矩阵乘法和激活函数的导数计算。

在多层神经网络的计算里，输入可以指代输入层或隐藏层，因为在这里被引入。输出层/隐藏层的矩阵在实现中应该被转置，后面会介绍。

    // Generate the Hidden Outputs
    Matrix inputs = fromArray(input_array);
    Matrix hidden = multiply(weights_ih, inputs);
    hidden.add_m(bias_h);
    hidden = sigmoidMatrix(hidden);

    // Generate output layer
    Matrix outputs = multiply(weights_ho, hidden);
    outputs.add_m(bias_o);
    outputs = sigmoidMatrix(outputs);

    // Convert array to matrix object
    Matrix targets = fromArray(target_array);

    // error = targets - outputs
    Matrix output_errors = subtract(targets, outputs);

    // gradient = outputs * (1 - outputs);
    Matrix gradients = dsigmoidMatrix(outputs);
    gradients.multiply_m(output_errors);
    gradients.multiply_n(learning_rate);

    // calculate deltas
    Matrix hidden_T = transpose(hidden);
    Matrix weights_ho_deltas = multiply(gradients, hidden_T);

    // adjust the weights by deltas
    weights_ho.add_m(weights_ho_deltas);
    // adjust the bias by its deltas (which is just the gradients)
    bias_o.add_m(gradients);

    // calculate the hidden layer errors
    Matrix who_t = transpose(weights_ho);
    Matrix hidden_errors = multiply(who_t, output_errors);

    // calculate the hidden gradient
    Matrix hidden_gradient = dsigmoidMatrix(hidden);
    hidden_gradient.multiply_m(hidden_errors);
    hidden_gradient.multiply_n(learning_rate);

    // calculate input->hidden deltas
    Matrix inputs_T = transpose(inputs);
    Matrix weights_ih_deltas = multiply(hidden_gradient, inputs_T);

    weights_ih.add_m(weights_ih_deltas);
    // adjust the bias by its deltas (which is just the gradients)
    bias_h.add_m(hidden_gradient);

上面的动画展示了一个简单的神经网络在训练过程中如何调整权重和偏置。每个方块代表一个输入数组，输出接近1的方块颜色会更深。动画从灰色开始，经过5000次训练后成功解决了XOR异或问题。

计算机的逻辑门由AND、OR、NOT和XOR异或门组成，它的输出为1当且仅当输入的两个值不相同。通过训练，神经网络学会了如何模拟这个逻辑门。两个神经元的组合可以模拟XOR异或门的行为，进而实现复杂的逻辑运算。

这也是由“单细胞生物”到“多细胞生物”的进化过程所实现的质的飞跃和巨大进步，因为它可以解决非线性可分问题。

对“由2个隐藏节点组成的网络结构”的直观理解：如果一个隐藏节点表示一条单一的分割线，2个表示2条，3个表示3条，依此类推…

将这个场景放入现实世界中，用平直砖块可以铺成任意形状的曲线。再放到数学世界，引入多层神经网络后，它可以很好地执行“曲线拟合”工作 :)

深度神经网络就是在做“曲线拟合”。

---

附录：

以下是 Caffe 的源代码，它在前向和反向计算中实现了 sigmoid：

namespace caffe {

template <typename Dtype>
inline Dtype sigmoid(Dtype x) {
  return 0.5 * tanh(0.5 * x) + 0.5;
}

template <typename Dtype>
void SigmoidLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
    const vector<Blob<Dtype>*>& top) {
  const Dtype* bottom_data = bottom[0]->cpu_data();
  Dtype* top_data = top[0]->mutable_cpu_data();
  const int count = bottom[0]->count();
  for (int i = 0; i < count; ++i) {
    top_data[i] = sigmoid(bottom_data[i]);
  }
}

template <typename Dtype>
void SigmoidLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
    const vector<bool>& propagate_down,
    const vector<Blob<Dtype>*>& bottom) {
  if (propagate_down[0]) {
    const Dtype* top_data = top[0]->cpu_data();
    const Dtype* top_diff = top[0]->cpu_diff();
    Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
    const int count = bottom[0]->count();
    for (int i = 0; i < count; ++i) {
      const Dtype sigmoid_x = top_data[i];
      bottom_diff[i] = top_diff[i] * sigmoid_x * (1. - sigmoid_x);
    }
  }
}